複素数の基本的な考え方を解説します。なぜ複素数という概念が生まれるのか。複素数はどの様に定義されたのか。これを読んで少しでも「複素数」というものについて納得できたら幸いです。
複素数の考え方
高校で複素数を勉強したことある人でも、大学から始めた人でも、複素数という新しい概念を受け入れられない人が多い。ただし、実はこのような新しい概念は今までもなんとなく受け入れてきたんです。この様に考えてみましょう。
もともと、世界には自然数という概念しかありませんでした。例えば、ものの個数を数えるときに用いられたりしました。
しかし、\(1-1\)や\(1-2\)とかの計算を成立させるためにゼロや負の数を取り入れた自然数を超えた新しい概念が必要でした。それが整数です。

次に、\(1\div2\)とかの計算を成立させるために、さらに整数を超えた概念を定義する必要がありました。それが有理数です。
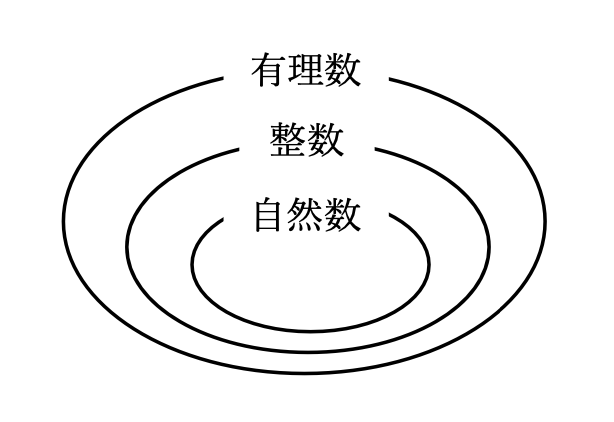
続いて、\(\sqrt{2}\)とかの分数では表せないような数を成立させるために、さらに無理数を加えた概念を作る必要がありました。それが私たちが今まで扱っていた実数です。
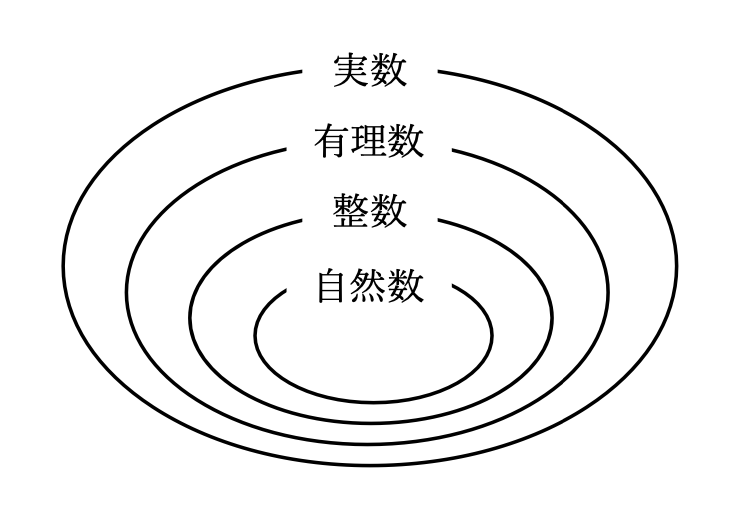
ここまでは広げた新しい概念を、私達はなんとなく受け入れてきました。自然数という概念しかなかった時代に\(\sqrt{2}\)とかいうものを説明しても、受け入れがたかったと思います。それと同じように、私達は二乗したら負になるような数、例えば\(\sqrt{-1}\)のような数を扱えるようにするために、虚数という新しい概念を取り入れる必要があるのです。それが複素数という概念です。
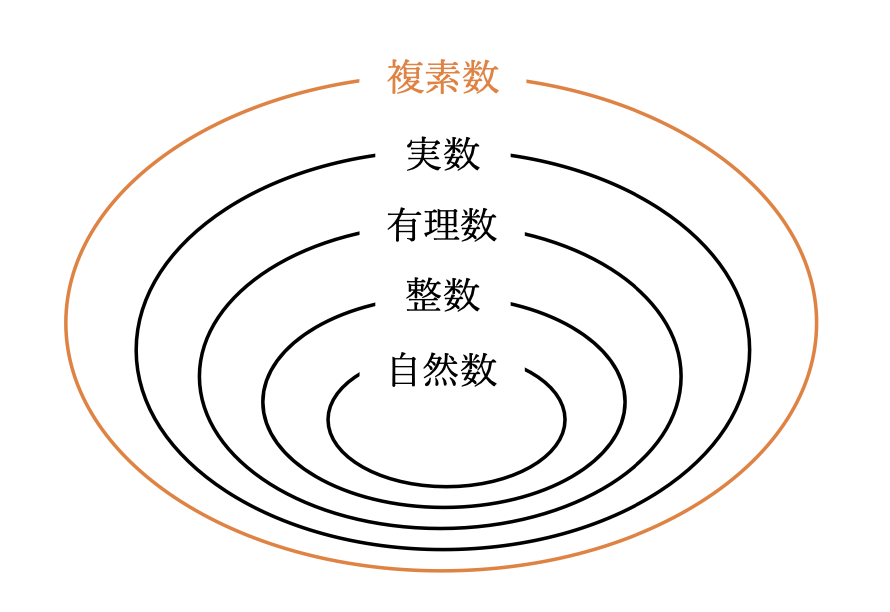
複素数を扱うまで、\(x^2=-1\)に対して「解なし」と答えていたのはあくまでも実数の範囲内でのことでした。そのため、最初に複素数という新しい概念について少しばかり違和感を感じてしまうのは無理もないことなのです。
複素数が\(a+bi\)で表される理由
結局、さらに大きな体系を定義するためにはそれまでの数も含めて全て網羅しなくてはなりません。例えば、整数は自然数を含むし、実数は有理数を含むようにです。そこで、複素数に実数を含ませるにはどのようにしたらいいのでしょうか。2も-2もまとめて整数と呼ばれたように、(\sqrt{2}\)も\(\sqrt{-2}\)もまとめて複素数と呼んでしまった方が楽の様に感じます。しかし、実はこれでは不都合が出てしまうのです。複素数を定義する目線に立って考えてみましょう。
実数まで、私達は数を数直線上で表すことができて、原点までの距離を可視化することができました。

しかし、この一本の数直線上では新しい概念である虚数を表すことができません。そこで、仕方なく次元を増やす方向で定義することにし、二次元で表すことにしました。この新たな二次元平面を複素平面、横向きの軸を実軸、縦向きの軸を虚軸と呼び、各軸上にある数をそれぞれ実数と虚数と呼ぶことにしたのです。また、虚数であることを目立たせるために、\(\sqrt{-1}=i\)と定義しました。

すると、ここで不都合が発生します。0から二つの直線が生えるという考え方、つまり二つの一次元の重なる部分であるという考え方では数学的におかしいからです。それよりも二次元の中の一点であると考えた方が明らかに自然でしょう。二次元にしたからにはこの平面の軸以外の部分も定義しなくてはなりません。
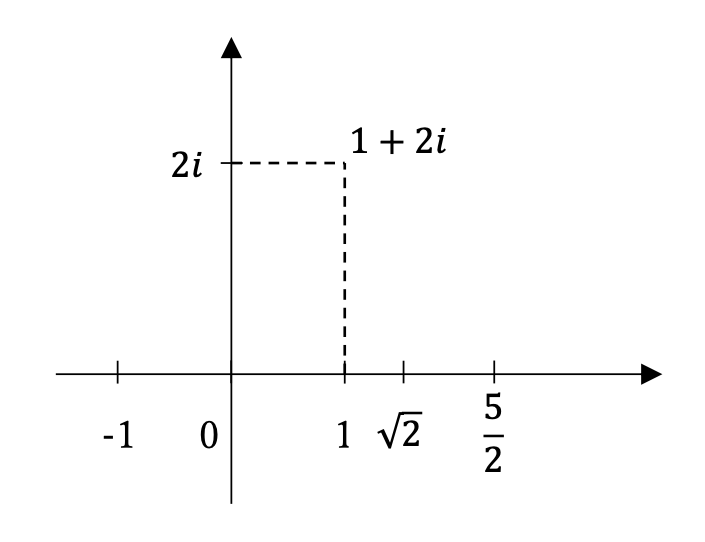
結局、二次元を使って表すと決めた以上、座標のように実数部分と虚数部分を同時に持つ様に定義するほかありません。ただし、座標と区別をするために実数部分と虚数部分をそれぞれ実部(Real part)と虚部(Imaginary part)と呼び、複素数\(z=a+bi\)に対して以下のように表ます。
$$a=\mathrm{Re}(z), ~b=\mathrm{Im}(z)$$
そして複素数を(実部)+(虚部)という形に定義したのです。ここで、実部と虚部という部分を表すような言葉通り、それらはあくまでも複素数という新しい数の一部分なのです。そして、実部のみからなる複素数を実数、虚部のみからなる複素数を純虚数と呼ぶことにしたのです。
他にも、計算や扱いの便宜上ある複素数\(z\)に対してその虚部の符号が逆の共役複素数\(\overline{z}\)を定義し、原点0からの距離を実数やベクトル同様に絶対値、そして0でない複素数\(z\)と原点0とを結ぶ線分と実軸の正の方向のなす角を\(z\)の偏角と名づけた。
これで無事、実数を含めた新たな数の概念を定義することができました。後は、演算を定義するだけだ。
複素数の演算の考え方
ある概念が導入されればその新しい数には新しい演算を定義しなくてはいけません。整数を定義したときに(負)x(負)=(正)と負の数という新しい数に対して新しい演算を定義したのと同じ様に、私達は複素数という新しい数に対して(純虚数)x(純虚数)=(実数)という新しい演算を定義しました。つまり、複素数の四則演算というのは\(i\times i=-1\)という新しいルールを実数の四則演算に加えることによって新たに導き出されるのです。
複素数の四則演算
\(z=a+bi, w=c+di \in \mathbb{C}\)とするとき
(1)\(a+bi=0:\iff a=b=0(\iff a^2+b^2=0)\)
(2)\(z\pm w := (a\pm c) + (b\pm d)i\)
(3)\(zw = (ac-bd) +(ad+bc)i\)
(4)\(w\neq 0\)のとき、\(\frac{z}{w}:=\frac{ac+bd}{c^2+d^2}+\frac{-ad+bc}{c^2+d^2}i\)
参考文献
- 川平友規.2019.『入門複素関数』.裳華房
