理系の大学生は一年目に線形代数を履修することになります。しかし、「線形代数」の意味がぼんやりしている状態で学んでは講義が進むにつれて「果たして何をしている学問なんだ?」と単なる計算作業の暗記になってしまいます。「線形代数」とは何か、「行列」とは何かをできるだけイメージしやすく解説してみましたので少しでも疑問が晴れたらこれから先の勉強が捗ります。
線形代数の意味
まず、「線形」というのは「直線」のことであり今までに習った1次関数というのは線形関数とも呼びます。
一方で、2次関数や3次関数など直線じゃないものは非線形です。
また、「代数」とは数字の代わりに文字を使うという意味です。例えば関数のx、yは代数です。
つまり「直線」を「文字」で表していろんな計算をする、というのが線形代数です。そして、線形代数で扱うのが行列です。
行列の意味
ここで、ベクトルというのは直線(矢印)であり、そのベクトルを新しいベクトルに変換するものを行列と言います。つまり、行列というのは直線の変換作業を行う関数なのです。例えば大きさを変えたり、向きを変えたりを行います。これを線形変換(一次変換)と言います。

これは一次関数\(y=kx\)と形が似ていますね。行なっていることは同様に、ある値を新しい値に変換しています。
これから線形代数を学んでいくと、連立方程式を解くためにこの考え方が応用されたり、いろんな使い方があります。
行列の表記方法
数字の組を表のように並べたものを行列と言います。この並びは配列とも呼びます。プログラミングなどでよく使われる呼び方ですね。また、横並びを「行」、縦並びを「列」と呼び、(行の数)×(列の数)をその行列の型と呼びます。
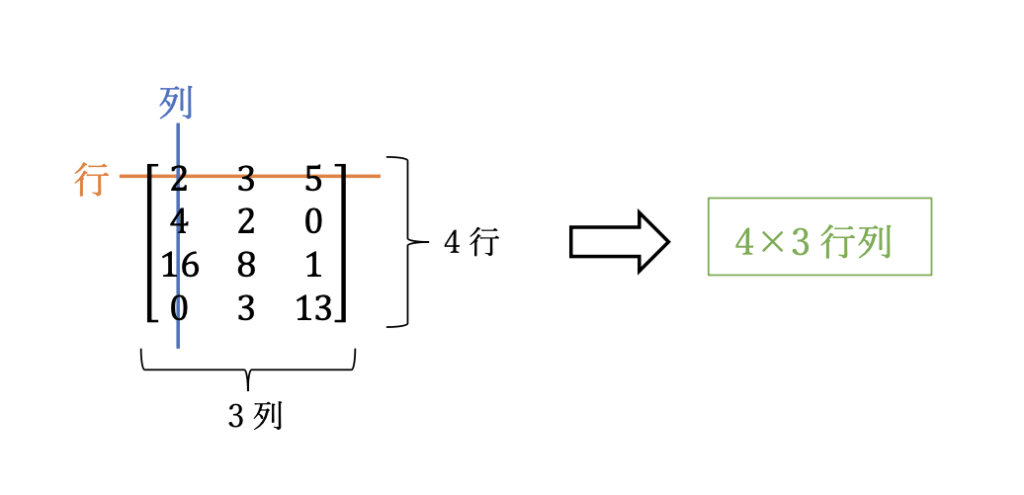
また、(特定の行,特定の列)にある値を成分と言います。
この行列の\((i, j)\)成分を\(a_{ij}\)と表記したりもします。
さらに、行と列の数が同じn個で構成されるn×n行列をn次の正方行列と呼びます。
他にも様々な行列がありますが、それらはすべてあるベクトルを新しいベクトルに変換させる(作用させるとも言う)関数であるというふうに解釈ができます。線形代数ではベクトルに作用させる行列という新しい関数を学んでいくことになります。
また、行列を文字で表すときにベクトルのようにボールド(太字)にする必要はなく、慣用的に大文字で表すことが多いです。
$$A=\begin{bmatrix}a&b\\c&d\end{bmatrix}$$
まとめ
- 線形代数は直線を文字で扱う数学分野。
- 行列はあるベクトルを新しいベクトルに変換する関数。
参考文献
- 高木悟・長谷川研二・熊ノ郷直人・菊田伸・森澤貴之.2023.『理工系のための線形代数』.培風館

