ベクトルの内積と絶対値の関係式や内積の計算を暗記で覚えてませんか?ベクトルの内積とその幾何的な意味を知ることで物理などの分野に活用できます。
ベクトルの内積
ベクトルの内積は次のように定義されています。
$$\boldsymbol{a}\cdot\boldsymbol{b}=|a||b|\cos\theta$$
※ベクトルとスカラーの概念にまだ不安がある方はこちらを確認しましょう。
このベクトルの内積と外積の関係は定義なので証明とかはありません。式の左辺はベクトル同士の掛け算のようですが、右辺はスカラーであることがわかります。よって、内積はベクトル同士を掛け算してスカラーにすることだと言えます。このことから内積はスカラー積とも呼びます。
ここで、スカラー同士の掛け算の演算子には\(\cdot\)か\(\times\)または省略しても意味は同じでしたが、ベクトル同士の計算においては\(\boldsymbol{a}\cdot\boldsymbol{b}\)が内積、\(\boldsymbol{a}\times\boldsymbol{b}\)が外積を表すので省略せず必ず使い分けが必要です。なお、スカラーとベクトルの掛け算もスカラー同士同様にどれを使っても大丈夫です。
内積の幾何的な意味
まずは先ほどの公式を図示してみましょう。
$$\boldsymbol{a}\cdot\boldsymbol{b}=|\boldsymbol{a}||\boldsymbol{b}|\cos\theta$$
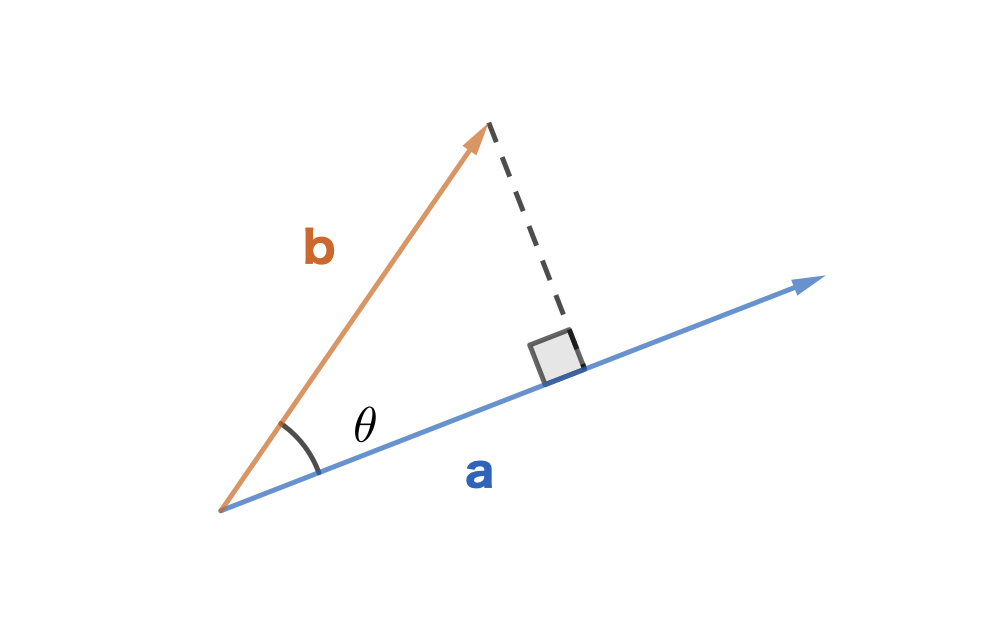
\(\cos\theta\)が\(|\boldsymbol{b}|\)に掛かっていると捉えた時、図をこのように書くと思います。この図と式を比較すると、内積というのは(\(\boldsymbol{b}\)の\(\boldsymbol{a}\)方向の成分の大きさ)と(\(\boldsymbol{a}\)の\(\boldsymbol{a}\)方向の成分の大きさ)の掛け算であることがわかります。これは\(\cos\theta\)が\(|\boldsymbol{a}|\)に掛かっていると捉えた時も同様です。
二つのベクトルが平行のとき
上を踏まえてベクトル同士が平行の時を考えてみましょう。図はこのようになります。
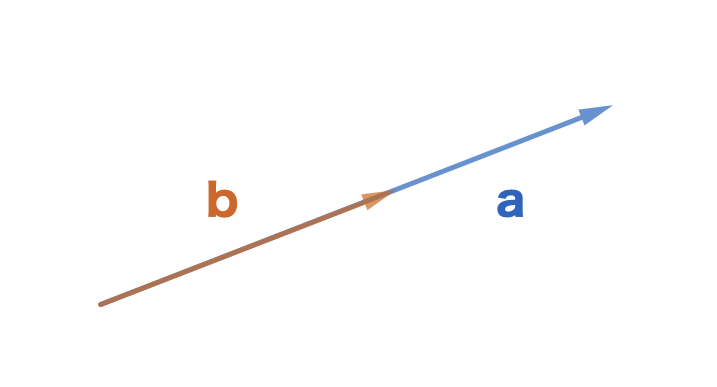
(\(\boldsymbol{b}\)の\(\boldsymbol{a}\)方向の成分の大きさ)はまさに\(\boldsymbol{b}\)の大きさそのものであり公式右辺の\(|\boldsymbol{a}||\boldsymbol{b}|\cos\theta\)は\(\boldsymbol{b}\)と\(\boldsymbol{a}\)の大きさ(つまり両ベクトルの絶対値)同士の掛け算になるはずです。
ここで、\(\theta=0^\circ\)を式に代入したら\(\boldsymbol{a}\cdot\boldsymbol{b}=|\boldsymbol{a}||\boldsymbol{b}|(∵\cos0^\circ=1)\)より確かに内積は二つのベクトルの絶対値(大きさ)同士の掛け算になっていますね。
二つのベクトルが垂直のとき
次にベクトル同士が垂直の時を考えてみましょう。図は以下の通りになります。
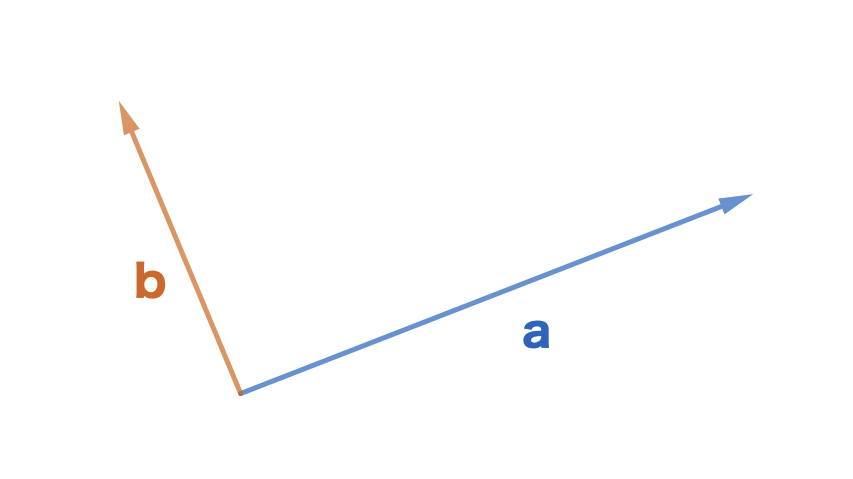
このように\(\boldsymbol{b}\)には\(\boldsymbol{a}\)方向の成分がありません。したがって(\(\boldsymbol{b}\)の\(\boldsymbol{a}\)方向の成分の大きさ)と(\(\boldsymbol{a}\)の\(\boldsymbol{a}\)方向の成分の大きさ)の掛け算は0になるはずです。
ここで、\(\theta=90^\circ\)を式に代入してみると\(\boldsymbol{a}\cdot\boldsymbol{b}=0(∵\cos0^\circ=1)\)より確かに内積は0になっています。
内積を使うことで何が嬉しいのか
内積を計算することで、ベクトル同士がどれだけお互いに影響し合っているのかスカラーで表せることにメリットがあります。2次元、3次元を超えた次元でも内積を用いることで数値的にベクトル同士の関係がわかります。ベクトル同士が平行であれば、互いにすべての成分が影響し合っていて(内積が大きさの積)、ベクトル同士が垂直であれば、互いに全く影響を及ぼしていません(内積が0)。この二つの異なるベクトルが互いにどのように影響するのかという定義は物理学で頻繁に使われます。
内積を使った具体例(仕事W)
物理学における仕事は、物体に加わる力ベクトルと、物体の変位ベクトルの内積によって定義されています。高校までの物理では仕事=移動距離×移動方向の力の大きさ、または仕事=力の大きさ×力が加わった向きに移動した距離だと教わったかもしれません。これってまさに(\(\boldsymbol{b}\)の\(\boldsymbol{a}\)方向の成分の大きさ)と(\(\boldsymbol{a}\)の\(\boldsymbol{a}\)方向の成分の大きさ)の掛け算、つまり内積なんですよね。
物体に与えた力と変位(移動方向と距離)は「向き」と「大きさ」を持つベクトル、物体にした仕事は「大きさ」のみを持つスカラーです。物体にした仕事\(W\)、物体に与えた力\(\boldsymbol{F}\)、変位\(\boldsymbol{r}\)とするとこのようなな関係式が成り立ちます。
$$\boldsymbol{F}\cdot\boldsymbol{r}=W$$
これも内積のベクトル・ベクトル=スカラーと同じ形をしていますね。そして、仕事とはまさに力と変位二つの異なるベクトル同士がお互いにどれだけ影響をしているのかを表していることがわかります。また、仕事の式は内積と同様に人類が都合よく決めた定義ですので証明はありません。この式が成り立つ理由が知りたい人は、物理学においてなぜこのように定義したら便利なのかを調べてみるといいかもしれません。
まとめ
- 内積\(\boldsymbol{a}\cdot\boldsymbol{b}=|\boldsymbol{a}||\boldsymbol{b}|\cos\theta\)とはベクトル同士の掛け算でスカラーになるように定義したもの。
- 内積とは二つの異なるベクトル同士の関係を示すもの。
- 仕事は内積で定義されている。

